Practice with the properties of real numbers The word NUMBERS implies the answer will deal only with numbers The word X implies the answer will contain a variable, but not necessarily the variable x A B Distributive Property (Numbers) 3 (5 2) = 15 6 Commutative Property of Addition (Numbers) 3 7 = 7 3 #(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2# We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence proved Show More Ex 25 Ex 25, 1 Ex 25,2 Important Ex 25,3 Important Ex 25,4

Expand 1 X Y 3 3 Solve It Fastly Brainly In
(x+y)^3 identity
(x+y)^3 identity-We shall use the identity for each bracketx 2 2 y 3 2 z 4 2 2 x 2 y 3 2 y 3 z 4 2 x 2 z 4 By arranging the like terms we get Now adding or subtracting like terms, Hence the value of is (ii) Given We shall use the identity x yz 2 = x 2 y 2 z 2 2 x y2 y z2 z x for expanding the brackets Now arranging liked terms we getSin (θ), Tan (θ), and 1 are the heights to the line starting from the x axis, while Cos (θ), 1, and Cot (θ) are lengths along the x axis starting from the origin The functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions



Www Jstor Org Stable
Prove the identity sin( 1 x) = sin(3 x) Question Prove the identity 3 cos(x y) 3 cos(x y) = 6 cos(x) cos(y) Use a Reciprocal Identity, and then rewrite as a single rational expression 7 tan(x) 7 tan(y) = 7 sin(y) cos(y) cos(x) = cos(x) cos(y) Use an Addition or Subtraction Formula to simplify Prove the identity sin( 1 xTherefore, x = 40 and y = 3 Given For all real numbers x and y such that x y = 3, the following identity hold axy bxcy 9 = 0 To find Value of a b c Solution For all real numbers x and y such that x y = 3, the following identity hold axy bxcy 9 = 0 as above identity holds for all real numbers x & y
To verify the identity a 3 b 3, we shall take a = 3 units and b = 1 unit Make an arrangement of 28 cubes such that we get a cube of 3 x 3 x 3 cubic units and a single unit cube of b = 1 unit as shown in fig (i) and fig(ii) Now we will use second set of 28 cubesXy 2 cos x y 2 sinx siny= 2sin x y 2 cos xy 2 cosx cosy= 2cos xy 2 cos x y 2 cosx cosy= 2sin xy 2 sin x y 2 The Law of Sines sinA a = sinB b = sinC c Suppose you are given two sides, a;band the angle Aopposite the side A The height of the triangle is h= bsinA Then 1If a(x1) (x2) = x 2 3x 2
Using the binomial expansion of (x y) ^3, we can write (x y)^3 = 1x^3 3x^2y 3xy^2 1y^3 where the coefficients come from the 3rd row of Pascal's triangle the first row = 1 = row "0" sosubstituting for x and y, we have (50 3)^3 = 1*50^3 3 (50)^2 (3) 3 (50) (3)^2 1*3^3 = 125,000 1350 27 =Here, Right hand side = Left hand side which means that (a3) (a3) is an identity Using Activity Method In this method, the algebraic identity is verified geometrically by taking different values of a x and y In the activity method, the identities are verified by cutting and pasting paper Find the value of 373 using the identity (x − y)3 = x3 − 3x2y 3xy2 − y3 Show all work Hint 373 = (40 − 3)3;



Www Jstor Org Stable




X Y 3 Identity Class 9 Novocom Top
Now substitue for a and b and u will get ur answer 1 = (x/2)3 (3x/y)3 3 * x/2 * 3x/y (x/2 3x/y) =x3/8 27/y3 9x2/4y 27x/2y3The algebraic identities for class 9 consist of identities of all the algebraic formulas and expressions You must have learned algebra formulas for class 9, which are mathematical rule expressed in symbols but the algebraic identities represent that the equation is true for all the values of the variables For example;Mentally examine the expansion of math(xyz)^3/math and realize that each term of the expansion must be of degree three and that because mathxyz/math is cyclic all possible such terms must appear Those types of terms can be represented




Solved A What Is The 2 Times 2 Identity Matrix I B Fin Chegg Com




Prove The Identity Simplify At Each Step 3 Cos X Chegg Com
Prove 3 cos(xy)3 cos(x trigonometricidentitycalculator Prove 3 cos(x y) 3 cos(x ar Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept An identity Since x − y = 3 xy=3 x − y = 3 implies y = x − 3, y=x3, y = x − 3, substituting this into the given identity gives a x (x − 3) b x c (x − 3) 9 = 0 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 \begin{aligned} ax(x3)bxc(x3)9&=0\\ ax^2(3abc)x3(c3)&=0 \end{aligned} a x (x − 3) b x c (x − 3) 9 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 = 0For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, the



Identity Vs Equation Acute Angel
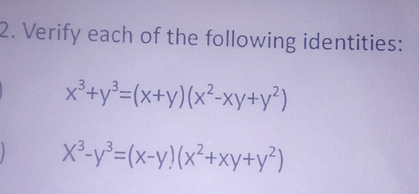



2 Verify Each Of The Following Identities X3 Y3 X Y X2 X Scholr
Using the identity a 3 − b 3 = (a − b) (a 2 b 2 a b) x 4 y 4 – x y = x y (x 3 y 3 − 1) = x y (x yPolynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2In mathematics, an identity is an equality relating one mathematical expression A to another mathematical expression B, such that A and B (which might contain some variables) produce the same value for all values of the variables within a certain range of validity In other words, A = B is an identity if A and B define the same functions, and an identity is an equality between




X Y 3 Identity Novocom Top
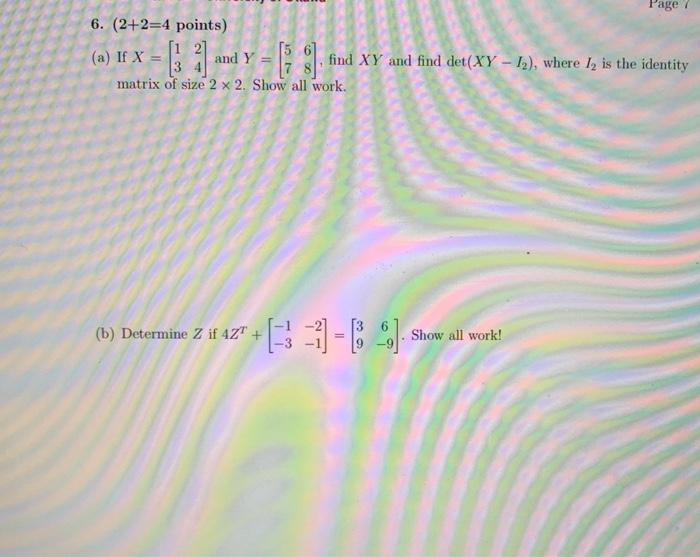



Page 6 2 2 4 Points 1 27 56 A If X And Y 3 Chegg Com
Let's Summarize The minilesson targeted in the fascinating concept of the cube of a binomial The math journey around the cube of binomial starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young mindsSolution Theorem 3 (a) and (b) THEOREM 3 (a) Law of Absorption yxx = x Proof yxx = yxx1 by identity (Ax 2b) = x (y1) by distributivity (Ax 4a) = x1 by Theorem 2 (a) = x by identity (Ax 2b) THEOREM 3 (b) x (xy) = x by duality Theorem 6 (a) and (b) THEOREM 6 (a) De Morgan's Laws (xy)' = x'y'In the expression, if we replace y with (− y), we will get the identity x 3 − y 3




Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts




Algebraic Identities Of Polynomials A Plus Topper
Solve (x/23/y) 3 Share with your friends Share 2 (a b) 3 = a 3 b 3 3a 2 b 3ab 2 , 1 ;Prove the identity 3 tan(x) 3 tan(cos(x) cos(y) 3 sin(x) Use a Reciprocal Identity, and then rewrite as a single rational expression 3 sin(y) cos(y) 3 tan(x) 3 tan(y) cos(x) cos(x) cos(y) Use an Addition or Subtraction Formula to simplifyIf 3x 2 = y and y = 8, then 3x 2 = 8 You might be torn here between the transitive property and the substitution property But what they did here was "cut out the middleman" by removing the " y " in the middle;




Entering Identities And The Problem Type Download Scientific Diagram



1
Therefore, x = 50 and y = 3Trigonometricidentitycalculator prove 3 cos(x y) 3 cos(x en Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept An identityActive Oldest Votes 2 If the neutral element is 0 and you want to find the inverse of a ∈ G, that means you want to find B such that 0 = a ∗ b This implies 0 = a ∗ G b = a × Q b Q a Q b = ( a Q 1) × ( b Q 1) − Q 1 1 = ( a Q 1) × Q ( b Q 1)




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




X Y 3 Identity Class 9 Novocom Top
They said that 3 x 2 = y = 8 , and then deleted the " y " in the middle, transiting right over it to create a new equationReplacing y with (−y) in the identity, (x y)3 = x3 3x2y 3xy2 y3Purplemath In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right trianglesThere are loads of trigonometric identities, but the following are the ones you're most likely to see and use




Verify The Following Identity X Y 3 X3 Y3 3xy X Y Brainly In




X Y X Y Which Of The Following Equation Must Be An Identity Z Y Z X Z Y Z X Y Teaching Mathematics Mathematical Objects
Proof Question How many 2letter words start with a, b, or c and end with either y or z?Y ×X 3 (y,x) 7−→φ(x,y) ∈ C is a sesquilinear form on Y ×X This map is referred to as the adjoint of φ For the remainder of this subsection we are going to restrict our attention to the case when X = Y In this case Lemmas 13 contain three easy but fundamental resultsThis algebraic identity can be written in the following form too ( a − b) 3 = a 3 − b 3 − 3 a 2 b 3 a b 2 Generally, the a minus b whole cubed algebraic identity is called by the following three ways in mathematics The cube of difference between two terms identity or simply the cube of difference identity The cube of a binomial formula




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




X Y 3 Identity Class 9 Novocom Top
View Full Answer a 3b 33ab(ab) 1 ;If x x x and y y y are real numbers such that x y = 7 xy=7 x y = 7 and x 3 y 3 = 133 x^3y^3=133 x 3 y 3 = 1 3 3, find the value of x y xy x y Submit your answer 3 3 ( 1640 ) 1 3 \sqrt{\sqrt{\sqrt3{\color{#3D99F6}{}} {\sqrt3{\color{#3D99F6}{} \color{teal}{3(1640) 1}}}}} 3 6 4 0 0 0 3 6 4 0 0 0 3 ( 1 6 4 0 ) 1Hi everyonein this video, I tell you about " x^3y^3=(xy)(x^2xyy^2) "?channel link https//wwwyoutubecom/channel/UC7Uui8og_cIpQaH9ItVWM3Q`````
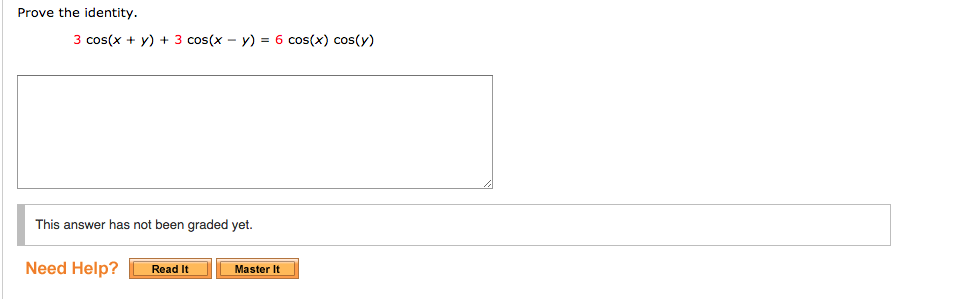



Prove The Identity Sin X Y Sin X Y 2 Cos X Chegg Com




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
This is an identity, it will work for any values of x and y Explanation There are several methods for solving simultaneous equations, but in this case I Straight Line Slope = 8000/00 = 4000 xintercept = 3/4 = yintercept = 3/1 = Rearrange Rearrange the equation by subtracting what is More ItemsSin (X 2π) = sin X , period 2π cos (X 2π) = cos X , period 2π sec (X 2π) = sec X , period 2π csc (X 2π) = csc X , period 2π tan (X π) = tan X , period π cot (X π) = cot X , period π Trigonometric Tables Properties of The Six Trigonometric Functions Graph, domain, range, asymptotes (if any), symmetry, x and yIt is read as $x$ plus $y$ whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ${(xy)}^3$ $\,=\,$ $x^3y^33x^2y3xy^2$ Proofs The cube of $x$ plus $y$ identity can be proved in two different mathematical approaches Algebraic method Learn how to derive the expansion of cube of $x$ plus $y$ identity by the




Companion Website Example Of Information Displayed If The Identity Download Scientific Diagram




Use A Suitable Identity To Fi See How To Solve It At Qanda
Given For all real numbers x and y such that x y = 3, the following identity hold axy bxcy 9 = 0 To find Value of a b c Solution For all real numbers x and y such that x y = 3, the following identity hold axy bxcy 9 = 0 Let say x = 3 => y = 0 as x y = 3We review their content and use your feedback to keep the quality high Transcribed image text Q2/ (A) Prove the identity tanAtanB = sin (AB) cosAcosB Q2/ (B) Find for the following equation y=3x) (3X) 3x Q2/ (A) Prove the identity tanAtanB = sin (AB) cosAcosB Q2/ (B) Find for the following equation y=3x) (3X) 3xElaborating x 3 y 3 using identity a 3 b 3 = (a b)(a 2 ab b 2) = x ( x y)(x 2 xy y 2) 3xy (x y ) Taking common x( x y ) in both the terms = x ( x y){x 2 xy y 2 3y} ∴ x (x 3 y 3) 3xy ( x y) = x ( x y )(x 2 xy y 2 3y)




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials



2
What is the identity of(ab) 3?What I hope to do in this video is prove the angle addition formula for sine or in particular prove that the sine of X plus y X plus y is equal to is equal to the sine of X sine of X times the cosine of sine of I forgot my X sine of X times the cosine of Y times the cosine of y plus cosine of X cosine of X times the sine of Y times the sine of Y and the way I'm going to do it is with this Ex 25, 9 Verify (i) x3 y3 = (x y) (x2 – xy y2) Ex 25, 9 Verify (ii) x3 y3 = (x y) (x2 xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x y




What Is The Formula Of Math A B 3 Math Quora




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube
(iii) (998) 3 = () 3 =1000 3 – 2 3 – 3x 1000x 2() Using identity (xy) 3 =x 3y 33xy (xy) =() = 8 – = Question 8 Factorise each of the followingSolution (x 3 8y 3 27z 3 – 18xyz)is of the form Identity VIII where a = x, b = 2y and c = 3z So we have, So we have, (x 3 8y 3 27z 3 – 18xyz) = (x) 3 (2y) 3 (3z) 3 – 3(x)(2y)(3z)= (x 2y 3z)(x 2 4y 2 9z 2 – 2xy – 6yz – 3zx)Answer 1 There are two words that start with a, two that start with b, two that start with c, for a total of \(222\text{}\) Answer 2 There are three choices for the first letter and two choices for the second letter, for a total of \(3 \cdot 2\text{}\)



1




Prove The Identity 3 Cos X Y 3 Cos X Y 6 Cos X Chegg Com
Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2) Find the value of 533 using the identity (x y)3 = x3 3x2y 3xy2 y3 Hint 533 = (50 3)3;X = 2 y = 2 # and print (x > 0 and y < 0) # True # or print (x > 0 or y < 0) # True # not print (not (x > 0 and y < 0)) # False Identity Operators Identity operators are used to check if two objects point to the same object, with the same memory location




X Y 3 X3 Y3 3xy X Y Brainly In




A Collection Of Algebraic Identities Pi Numbers
This video shows how to expand using the identity '(xy)3=x3y33x2y3xy2'To view more Educational content, please visit https//wwwyoutubecom/appuseriesaGiven a sesquilinear form φ on X ×Y, prove that the map φ?




Factorise 27 X Y 3 8 X Y 3 Maths Polynomials Meritnation Com
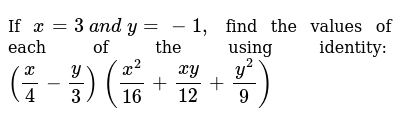



If X 3 A N D Y 1 Find The Values Of Each Of The Using Identi



1




Facorize X X Y 3 3x 2y X Y




Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks
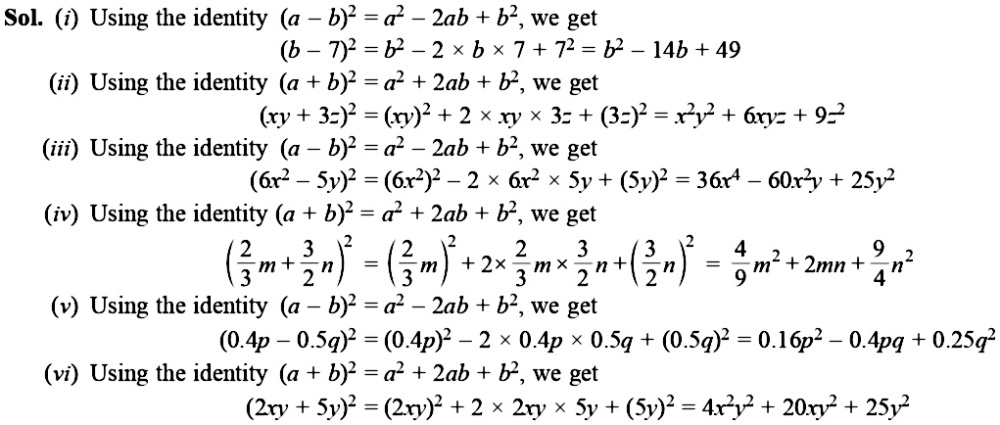



Find The Following Squares By Using The Identities I B 7 2 Ii Xy 3z 2 Iii 6x 2 5y 2 Iv Frac 2 3 M Frac 3 2 N 2 V 0 4p 0 5q 2 Vi 2xy 5y 2 Snapsolve




Pdf Two Theta Function Identities Of Level 10




Prove X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Brainly In




Binomial Theorem Wikipedia




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




X Y 3 Identity Novocom Top



What Is The Answer Of X Y Quora




X Y 3 Identity Novocom Top




Untitled Bingo Card




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Ppt Polynomials Powerpoint Presentation Free Download Id




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




Polynomials Ppt Video Online Download
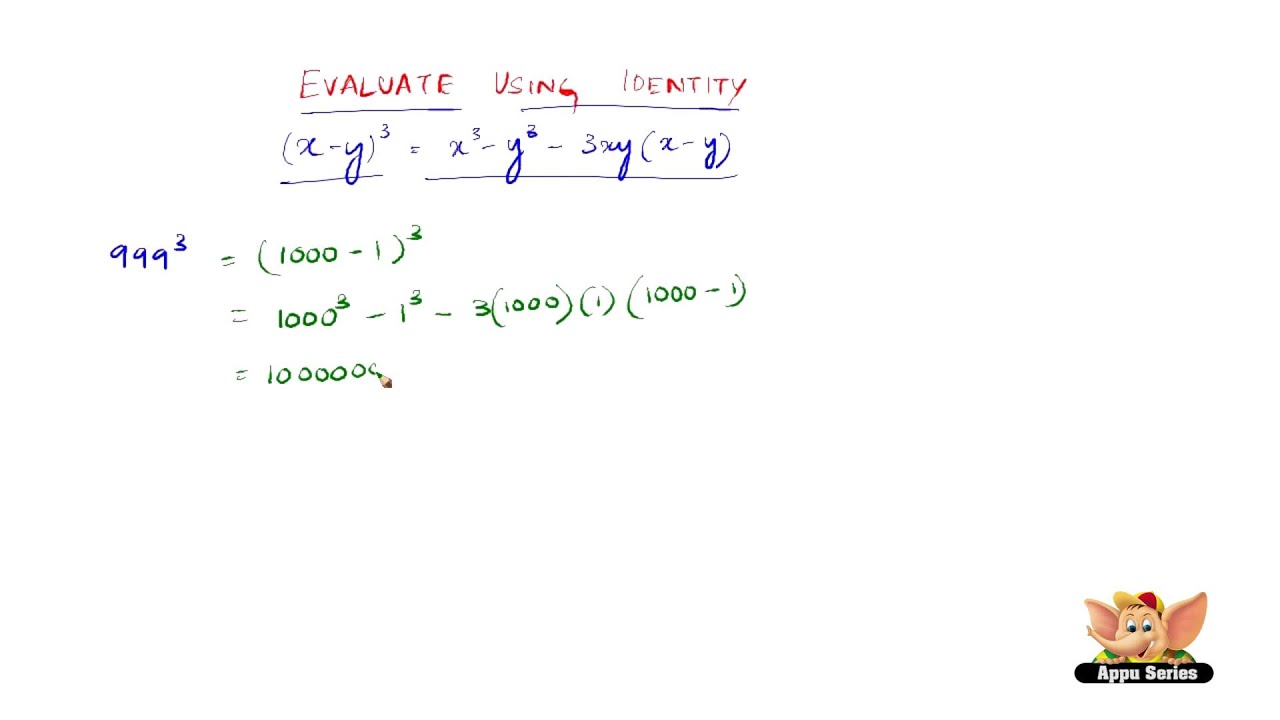



How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




What Are The Factors Of X Y 3 X3 Y3 Brainly In




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Answered Prove The Polynomial Identity For The Bartleby



Find The Following Squares By Using Identities I B 7 2 Ii Xy 3z 2 Sarthaks Econnect Largest Online Education Community




Ex 9 5 3 Find The Squares By Using Identities I B 7 2




X 3 Y 3 X 3 Y 3 Formula Proof Youtube




Shashanktutorial Shashank Tutorial




Prove The Identity 3 Cos X Y 3 Cos X Y 6 Chegg Com




Algebraic Identities Of Polynomials A Plus Topper




2 Solve It Plz Q If X Y 10 And Xy 21 Find The Value Of X3 Y3 Using Identity Maths Polynomials Meritnation Com




Expand 1 X Y 3 3 Solve It Fastly Brainly In




Find The Following Squares By Using The Identities I B 7



1




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55




Math Garden Binomial Identity




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
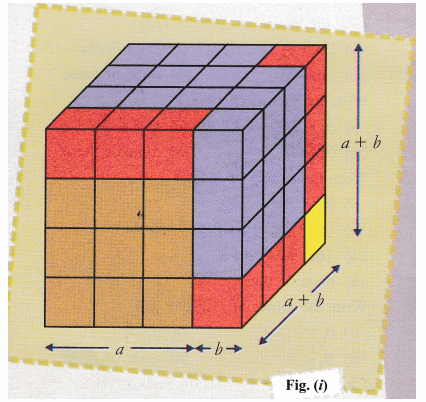



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Lines And Am Nles




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Prove That 1 1 1 X Y Z X 3 Y 3 Z 3 X Y Y Z X Y Z
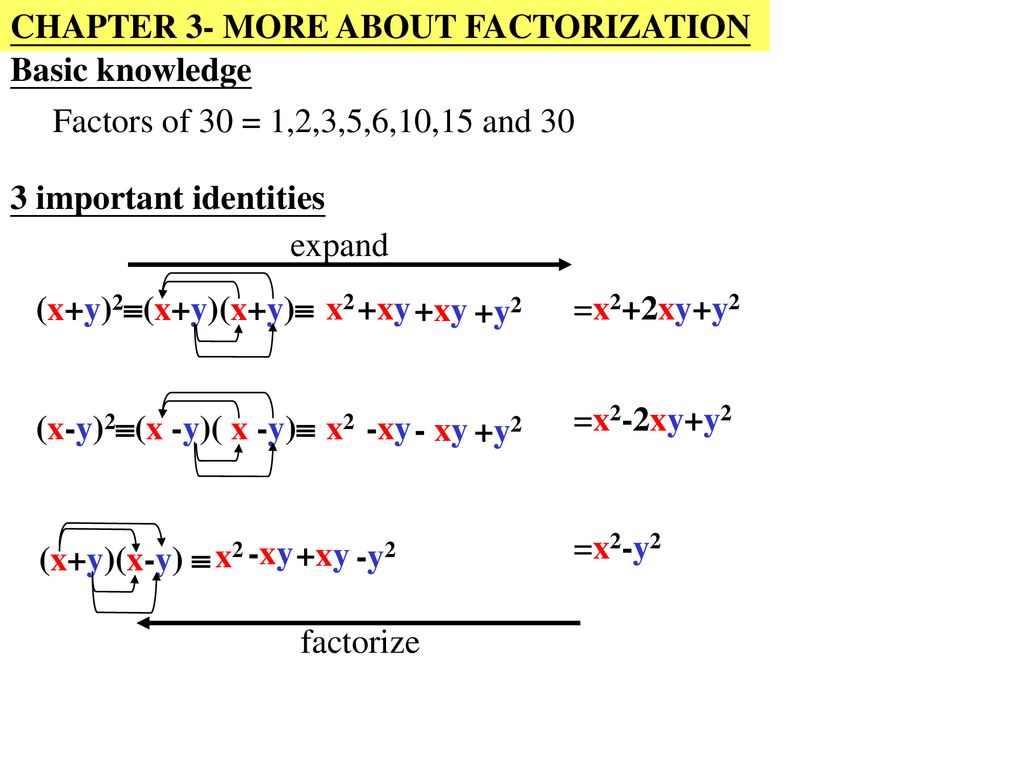



Chapter 3 More About Factorization Ppt Download




If X 3 A N D Y 1 Find The Values Of Each Of The Using Identi




How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com




Pdf On Trace Forms On A Class Of Commutative Algebras Satisfying An Identity Of Degree Four



Expand 1 X Y 3 Whole Cube Studyrankersonline




If X Y Z 0 Then Find The Value Of X 3 Y 3 Z 3 Maths Algebraic Expressions And Identities Meritnation Com




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Using Identities Prove That X Y Z 2 3 Xy Yz Zx Where X Y Z Are Positive Real Numbers Maths Polynomials Meritnation Com




Example 8 Multiply I X 4 And 2x 3 Ii X Y 3x 5y




3 Simplify The Following Functional Expressions Chegg Com




List Of Trigonometric Identities Wikipedia




Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8




Polynomials Ppt Video Online Download




Ppt Polynomials Powerpoint Presentation Free Download Id




Derive An Identity For X Y 3 Brainly In



Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Www Topperlearning Com Answer Using Identities Prove That X Y Z 2 3 Xy Yz Zx Where X Y Z Are Positive Real Numbers 3gc3fduu




Given A X 3 Y 3 If A 3i Where I Is The Identity Matrix Of Order 2 Find X And Y Brainly In




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



Identity Mathematics Wikipedia




Pdf Antiflexible Rings With Identity X Y X 0 M Hema Prasad Academia Edu




Algebraic Identities 6 And 7 Youtube




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Algebraic Identities Of Polynomials A Plus Topper
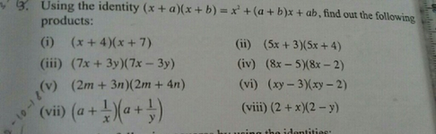



V3 Using The Identity X A X B X A B X Ab Find Ou Scholr




Learn Algebraic Identities Of X Y And X Y In 3 Minutes



No comments:
Post a Comment